Latihan Soal Sifat - Sifat Gradien Pada Persamaan Garis Lurus Matematika Kelas 8 Kurikulum 2013 dan Pembahasannya ini terdiri dari soal tentang sifat gradien. Gradien adalah tingkat kemiringan suatu garis, yang disimbolkan dengan m.
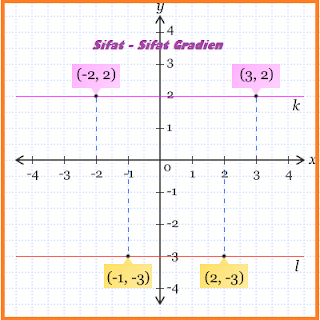
Sifat - Sifat Gradien :
- Gradien garis yang sejajar dengan sumbu-x, m = 0
- Garis yang sejajar dengan sumbu-y tidak memilki gradien
- Gradien dua garis yang sejajar adalah sama, m1 = m2
- Gradien dua garis yang tegak lurus, m1 x m2 = -1
Berikut ini beberapa contoh Latihan Soal Gradien pada Persamaan Garis Lurus Kelas 8 Kurikulum 2013 dan Pembahasannya:
Tentukan apakah kedua garis tersebut sejajar atau tegak lurus?
a. Garis k yang melalui titik A(7, -3) dan B(11, 3)
Garis l yang melalui titik C(-9, 0) dan D(-5, 6)
b. Garis m yang melalui titik P(3, 5) dan Q(0,0)
Garis n yang melalui titik R(0, 0) dan S(-5, 3)
Pembahasan:
a. Mencari gradien garis k
Untuk titik A(7, -3), maka x1 = 7 dan y1= -3
Untuk titik B(11, 3), maka x2 = 11 dan y2 = 3.
mAB = y2 - y1
x2 - x1
mAB = 3 - (-3)
11 - 7
mAB = 3+3/4
mAB = 6/4
Mencari gradien garis l
Untuk titik C(-9, 0), maka x1 = -9 dan y1= 0
Untuk titik D(-5, 6), maka x2 = -5 dan y2 = 6.
mCD = y2 - y1
x2 - x1
mCD = 6 - 0
-5 - (-9)
mCD = 6/-5+9
mCD = 6/4
Karena mAB = mCD = 6/4, maka garis k dan l sejajar.
b. Mencari gradien garis m
Untuk titik P(3, 5), maka x1 = 3 dan y1= 5
Untuk titik Q(0,0), maka x2 = 0 dan y2 = 0.
mPQ = y2 - y1
x2 - x1
mPQ = 0 - 5
0 - 3
mPQ = -5/-3 = 5/3
Mencari gradien garis n
Untuk titik R(0, 0), maka x1 = 0 dan y1= 0
Untuk titik S(-5, 3), maka x2 = -5 dan y2 = 3.
mRS = y2 - y1
x2 - x1
mRS = 3 - 0
-5 - 0
mRS = 3/-5
Karena mPQ x mRS = -1
5/3 x 3/-5 = -1, maka garis m dan n saling tegak lurus.
Soal Ulangan Harian Persamaan Garis Lurus Kelas 8 Kurikulum 2013 dan Pembahasannya