Soal Ulangan Harian Persamaan Garis Singgung Lingkaran Matematika SMA/MA Kelas 11/XI Kurikulum 2013 dan Pembahasannya - ini merupakan contoh soal ulangan harian/ Penilaian Harian (PH) terbaru yang akan kami bagikan pada kesempatan kali ini. Persamaan garis singgung lingkaran adalah suatu garis yang menyinggung suatu lingkaran. Dalam postingan ini berisi latihan soal tentang cara menentukan persamaan garis singgung lingkaran.
Berikut ini contoh Soal Ulangan Harian Persamaan Garis Singgung Lingkaran Matematika Kelas 11/XI Kurikulum 2013 dan Pembahasannya:

Soal No. 1
Diberikan persamaan lingkaran:
L ≡ x2 + y2 = 25.
Tentukan persamaan garis singgung lingkaran yang memiliki titik singgung di (−4, 3).
Pembahasan
Menentukan garis singgung pada suatu lingkaran yang pusatnya di (0, 0) dan diketahui titik singgungnya.
Lingkaran L ≡ x2 + y2 = r2
Titik singgung (x1, y1)
Persamaan garis singgungnya adalah:
Dengan x1 = − 4 dan y1 = 3, persamaan garisnya:
−4x + 3y = 25
3y −4x − 25 = 0
Soal No. 2
Salah satu persamaan garis singgung lingkaran x2 + y2 = 25 yang tegak lurus garis 2y − x + 3 = 0 adalah....
Pembahasan
Garis 2y − x + 3 = 0 memiliki gradien sebesar 1/2. Garis lain yang tegak lurus dengan garis ini harus memiliki gradien − 2. Ingat pelajaran SMP 8, jika dua garis saling tegak lurus maka berlaku
m1 ⋅ m2 = − 1
Sehingga persamaan garis singgung di lingkaran x2 + y2 = 25 yang memiliki gradien −2 adalah:
 Jadi persamaan garis singgungnya bisa y = −2x + 5√5 bisa juga y = −2x − 5√5, pilih yang ada.
Jadi persamaan garis singgungnya bisa y = −2x + 5√5 bisa juga y = −2x − 5√5, pilih yang ada.Diberikan persamaan lingkaran:
L ≡ (x − 2)2 + (y + 3)2 = 25
Tentukan persamaan garis singgung lingkaran dengan titik singgung pada (5, 1).
Pembahasan
Persamaan garis singgung pada lingkaran:
L ≡ (x − a)2 + (y − b)2 = r2
pada titik singgung (x1, y1)
dengan a = 2 dan b = −3 dan r2 = 25
maka persamaan garisnya


Untuk lebih lengkapnya, silakan klik tautan berikut:



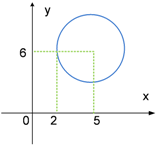

 dengan n bilangan bulat.
dengan n bilangan bulat.
 dibaca akar pangkat 2 dari 9,
dibaca akar pangkat 2 dari 9, ,
,
 adalah....
adalah....
 adalah....
adalah....
 adalah....
adalah....